10651. Наименьшая
топологическая сортировка
Задан
ориентированный невзвешенный граф. Найдите его лексикографически наименьшую
топологическую сортировку.
Вход. В
первой строке заданы два целых числа n
и m
(1 ≤ n, m ≤ 105) – количество вершин и рёбер в графе. В
следующих m строках перечислены рёбра
графа. Каждое ребро задается парой чисел – номерами начальной и конечной
вершин.
Выход. Выведите
лексикографически наименьшую топологическую сортировку графа в виде
последовательности номеров вершин. Если топологическую сортировку выполнить
невозможно, выведите -1.
|
Пример
входа |
Пример
выхода |
6 61 23 24 22 56 5
4 6 |
1 3 4 2 6 5 |
РЕШЕНИЕ
графы –
топологическая сортировка
Анализ алгоритма
В задаче требуется
найти лексикографически наименьшую топологическую сортировку. Воспользуемся
алгоритмом Кана (Kahn). Вместо классической очереди будем использовать очередь
с приоритетом или множество.
Сначала добавим в
очередь все вершины, в которые не входят рёбра (такие вершины могут начинать
топологическую сортировку). На каждой итерации будем извлекать из очереди
наименьший элемент – это обеспечит построение лексикографически наименьшей
топологической сортировки.
Пример
Граф, приведенный в примере, имеет
следующий вид:
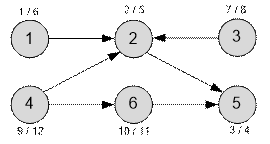
Данный граф допускает
несколько вариантов топологической сортировки. Например:
·
1, 4, 6, 3, 2, 5;
·
4, 3, 6, 1, 2, 5;
·
3, 1, 4, 2, 6, 5;
Лексикографически наименьшей топологической
сортировкой является
1, 3, 4, 2, 6, 5
Лексикографически наибольшей топологической
сортировкой является
4, 6, 3, 1, 2, 5
Реализация алгоритма – set
Входной граф храним в
виде списка смежности g. Входящие степени вершин храним в
массиве InDegree. Топологически отсортированные вершины графа
заносим в массив Order.
vector<vector<int> > g;
vector<int> InDegree, Order;
set<int> minHeap;
Читаем входной граф.
scanf("%d %d", &n,
&m);
g.resize(n + 1);
InDegree.resize(n + 1);
Вычисляем входящие степени для всех вершин. Для каждого ребра (a, b)
увеличиваем значение входящей степени вершины b.
for (i = 0; i < m; i++)
{
scanf("%d %d", &a, &b);
g[a].push_back(b);
InDegree[b]++;
}
Все вершины с нулевой входящей степенью добавляем во множество minHeap.
for (i = 1; i < InDegree.size(); i++)
if (InDegree[i] == 0) minHeap.insert(i);
Продолжаем работу алгоритма топологической сортировки, пока множество minHeap не
станет пустым.
while (!minHeap.empty())
{
Извлекаем из minHeap вершину v с наименьшим номером и
добавляем её в конец топологического порядка.
v = *minHeap.begin();
minHeap.erase(minHeap.begin());
Order.push_back(v);
Удаляем из графа все рёбра (v, to), исходящие из вершины v. Для каждого такого ребра уменьшаем
входящую степень вершины to. Если входящая степень вершины to
становится нулевой, добавляем её в множество, откуда она попадёт в список
топологического порядка.
for (int to : g[v])
{
InDegree[to]--;
if (InDegree[to] == 0)
minHeap.insert(to);
}
}
Если после выполнения алгоритма в массив Order добавлены не все n
вершин, то граф содержит цикл, и топологическая сортировка невозможна.
if (Order.size() < n)
printf("-1");
else
Выводим вершины графа в лексикографически наименьшем топологическом
порядке.
for (i = 0; i < Order.size(); i++)
printf("%d ", Order[i]);
printf("\n");
Реализация алгоритма – priority
queue
#include <cstdio>
#include <queue>
#include <vector>
using namespace std;
vector<vector<int> > g;
vector<int> InDegree, Order;
priority_queue<long long, vector<long long>, greater<long long> > pq;
int i, n, m, a, b, v, to;
int main(void)
{
scanf("%d %d", &n, &m);
g.resize(n + 1);
InDegree.resize(n + 1);
for (i = 0; i < m; i++)
{
scanf("%d %d", &a, &b);
g[a].push_back(b);
InDegree[b]++;
}
for (i = 1; i < InDegree.size(); i++)
if (InDegree[i] == 0) pq.push(i);
while (!pq.empty())
{
v = pq.top(); pq.pop();
Order.push_back(v);
for (int to : g[v])
{
InDegree[to]--;
if (InDegree[to] == 0) pq.push(to);
}
}
if (Order.size() < n)
printf("-1");
else
for (int x : Order)
printf("%d ", x);
printf("\n");
return 0;
}
Java реализация – priority
queue
import java.util.*;
import java.io.*;
public class Main
{
static
ArrayList<ArrayList<Integer>> g;
static ArrayList<Integer> top;
static int InDegree[];
static int n, m, flag = 0;
public static void main(String[] args)
{
FastScanner con = new FastScanner(System.in);
n = con.nextInt();
m = con.nextInt();
g = new
ArrayList<ArrayList<Integer>>();
InDegree = new int[n+1];
for (int i = 0; i <= n; i++)
g.add(new ArrayList<Integer>());
for (int i = 0; i < m; i++)
{
int a = con.nextInt();
int b = con.nextInt();
g.get(a).add(b);
InDegree[b]++;
}
PriorityQueue<Integer> pq = new PriorityQueue<Integer>();
for(int i = 1; i <= n; i++)
if (InDegree[i] == 0) pq.add(i);
top = new ArrayList<Integer>();
while (!pq.isEmpty())
{
int v = pq.poll();
top.add(v);
for (int to : g.get(v))
{
InDegree[to]--;
if (InDegree[to] == 0) pq.add(to);
}
}
if (top.size() < n)
System.out.println("-1");
else
{
for (int x : top) System.out.print(x + " ");
System.out.println();
}
}
}
class FastScanner
{
BufferedReader br;
StringTokenizer st;
public FastScanner(InputStream inputStream)
{
br = new BufferedReader(new InputStreamReader(inputStream));
st = new StringTokenizer("");
}
public String next()
{
while (!st.hasMoreTokens())
{
try
{
st = new StringTokenizer(br.readLine());
} catch (Exception e)
{
return null;
}
}
return st.nextToken();
}
public int nextInt()
{
return Integer.parseInt(next());
}
}
Python реализация – priority queue
Импортируем функции heappush и heappop из модуля heapq. heapq – это встроенная библиотека Python, которая предоставляет
реализацию очереди с
приоритетами на основе кучи.
from heapq import heappush, heappop
Читаем количество
вершин n и ребер m в графе.
n, m = map(int, input().split())
Входной граф храним в
виде списка смежности g. Входящие степени вершин храним в
массиве InDegree.
g = [[] for _ in
range(n + 1)]
InDegree = [0] * (n + 1)
Читаем входной граф. Вычисляем входящие степени для всех вершин. Для
каждого ребра (a, b) увеличиваем значение входящей степени
вершины b.
for _ in range(m):
a, b = map(int, input().split())
g[a].append(b)
InDegree[b] += 1
Все вершины с нулевой входящей степенью добавляем в список minHeap.
minHeap = []
for i in range(1, len(InDegree)):
if InDegree[i] == 0:
heappush(minHeap, i)
Топологически
отсортированные вершины графа заносим в массив Order.
Order = []
Продолжаем работу алгоритма топологической сортировки, пока список minHeap не
станет пустым.
while minHeap:
Извлекаем из minHeap вершину v с наименьшим номером и
добавляем её в конец топологического порядка.
v = heappop(minHeap)
Order.append(v)
Удаляем из графа все рёбра (v, to), исходящие из вершины v. Для
каждого такого ребра уменьшаем входящую степень вершины to.
Если входящая степень вершины to становится
нулевой, добавляем её в очередь, откуда она попадёт в список топологического
порядка.
for to in g[v]:
InDegree[to] -= 1
if InDegree[to] == 0:
heappush(minHeap, to)
Если после выполнения алгоритма в массив Order добавлены не все n
вершин, то граф содержит цикл, и топологическая сортировка невозможна.
if len(Order) < n:
print(-1)
Выводим вершины графа в лексикографически наименьшем топологическом
порядке.
else:
print(*Order)